Deltas in pixel space are very different than deltas in concept space

Our quandary

Sometimes in RL, we want to (don’t worry about why) measure the difference between a pair of states. I think it’s fair to say that we have a general intuition for what makes two things different in meaningful ways for a given context, and ideally we’d like the math of our methods to match our expectations for that.

The problem is that some methods will often fail the intuition test badly, implying we need better methods. Let’s see why!

Where it’s all good

Call the pair of states $(s_1, s_2)$, each a vector of length $N$, and call our scalar difference (delta) between them $\Delta$.

A very natural thing to do would be to just define $\Delta$ as the MSE: \(\Delta(s_1, s_2) = \|s_1 - s_2 \|^2\) Sometimes this “naive approach” will work just fine. If our states are in a 2D gridworld environment where each state is an $[x, y]$ pair of the cell coordinates, like this for example:

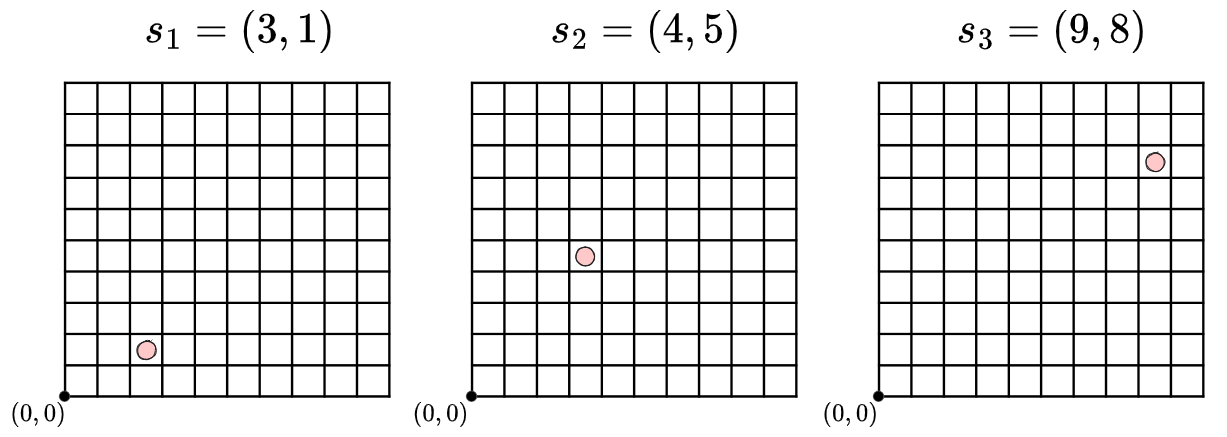
and we calculate the deltas (ignoring the constant mean factor), we’d get: \(\Delta(s_1, s_2) = \|s_1 - s_2 \|^2 = (1^2 + 4^2) = 17\) \(\Delta(s_1, s_3) = \|s_1 - s_3 \|^2 = (6^2 + 7^2) = 85\) and this matches our expectation: The difference between $s_1$ and $s_2$ is a lot bigger than the difference between $s_1$ and $s_3$.

Where it’s not so good

Now let’s say instead of a simple gridworld, we have a house tidying robot. Its state space is raw images from its camera. For our mystery unspecified reason, we supply it with an image (the “target image”) and we want it to measure how different its current camera image is from the target image in meaningful ways we care about.

For example, maybe we give it a target image that’s a view of a scene in the house, and it’s programmed such that when it finds a view from its own camera such that the delta with the target image is below some threshold, it starts violently tidying.

Here’s our target image:

Now, which of the following robot camera images has the smallest difference with the target image?

This one, where an adorable puppy named Goose has sat down on the chair?

Or this one, which is exactly the target image scene, but much brighter because the photo was taken at midday with bright sunlight?

Or this one, also exactly the target, but taken in the evening when everything is a bit dimmer?

To compare them side by side, hopefully we agree that for the current context, this pair:

is meaningfully less different than this pair:

I mean, the camera in the top pair is exactly what we want it to clean, it just happens to be brighter. Surely a smart robot should be able to deal with that.

OTOH, the bottom one is totally different – it has a ridiculously cute dog in it! If our tidying robot decides the image with the wiggliest ragamuffin is close enough to the target image, who’s to say it won’t start tidying everything in the scene? 🥺

And yet, with the naive delta calculation from above, we’d find that the bottom pair is supposedly less different than the top pair!

Diffs

To see this, let’s do the following:

• Convert all the images to grayscale
• Take the difference with the target image
  • and save the image that’s the absolute value of this difference image
• Take the mean (across all the pixels) of the square of this difference, which is our naive delta from above

Basically this code snippet:

target_image = Image.open(target_image_path).convert("L")  # Convert to grayscale
other_image = Image.open(other_image_path).convert("L")
target_array = np.array(target_image).astype(np.float32)
other_array = np.array(other_image).astype(np.float32)
abs_diff = np.abs(target_array - other_array)  # save this image
delta = np.mean(abs_diff**2)
print(f"\n{delta = :.1f}")

aaaand we get:

img_goose_error = 1806.9
img_no_goose_light_error = 7074.3
img_no_goose_dark_error = 5858.4

i.e., the one with Goose has a significantly smaller delta!

To see this, below are the abs diff images (where black is 0, white is 1) for each.

Goose vs target:

You can see that:

• there’s a ghostly doggy where she sat,
• the diff image has a bit of an edge finding effect, since I accidentally moved the camera a bit in between shots, and
• most of the image aside is black, meaning little difference

Here are the abs diff images for the extra-light and extra-dark images:

You can see for both of these that although they don’t have any sharp differences the way the one with Goose has (and they might even have smaller max differences), they’re nearly entirely white or gray (meaning, larger differences), because the extra lightness or darkness has affected nearly the whole image.

Sure, but what if we try…

Hopefully the above example illustrates why the naive version sometimes fails. In this case, in terms of pixels, the meaningful difference is kind of “peakier”, but the non-meaningful differences are more widespread across the image and really add up.

But you might say, okay, what if we just handle cases like this, by doing things like also using the max of the abs diff? or, comparing them in frequency space? or, maybe we could first normalize the images to have the same mean brightness as the target image?

These might all be good ideas for other reasons, but they’re really just kicking the can down the road, and the real problem calls for something else.

“Meaningful” isn’t very meaningful in a vacuum

Yeah, you’re sooo clever and probably already saw this coming two paragraphs in, but the crux here is the weasel word “meaningful” I’ve been using a lot. I.e., we said that this pair:

was “incorrectly” ranked as more meaningful than the one with Goose. And, maybe in the context of the tidying robot, this is fair: we don’t want it tidying up the dog.

But what if, instead of a tidying robot, it was a smart home device that waits until the ambient light levels get high or low enough compared to a reference image, to activate something? In that case, it’d be irrelevant if a sweet pup were in the scene, and we really would care about the broad lightness or darkness of the image.

Basically, “meaningful” is going to be extremely problem-specific; in some problems we’re going to want it to completely ignore aspects that would be major differences in other problems. Our robot could care only about high level contents of the image, like whether a given book is in the image or not. So, this calls for better methods that can take these general differences into account.

Deep learning, says captain obvious

Basically, the real problem here is trying to rank differences between image pairs in terms of pixels in the first place. Whatever a “meaningful” difference means for our use-case, the point is that it’s a conceptual difference and we’d be fools to try and do it on the pixel level.

And this is kind of obvious and one of the main reasons we do deep learning in the first place. We could just train a deep learning model that takes in two images and outputs a difference score, and train it with positive and negative examples a la contrastive learning.

However, I’ll end with one little wrinkle that’s less obvious, as a teaser for future posts:

We could do what I just mentioned and make a NN model $f(s_1, s_2)$ that outputs a real scalar number representing the difference between the pair $(s_1, s_2)$. But, we often don’t only want this number; we do want to be able to calculate it, but we also want to have some representation of the inputs that obeys this relationship.

To get this, a common technique is to train an embedding with this constraint, and then you can embed inputs and know that in that space, they have this structure you want. For example, instead making a model $f(s_1, s_2)$ directly output the correct scalar difference, we could create a NN model that’s an embedding $z = \phi(s)$ (where $z$ is a vector), and then say $f(s_1, s_2) = |\phi(s_1) - \phi(s_2)|^2$ or $f(s_1, s_2) = \phi(s_1)^T \phi(s_2)$. Then, we’d still train $f(s_1, s_2)$ on to match the correct scalar difference, but it’d really be training $\phi(s)$.